Junio

GRAFICAS Y CURVAS DE NIVEL


para representar la grafica de una funcion f(x,y) se requiere de un sistema coordenado (x,y,z) de R3


DEFINICION
si f es una funcion de 2 variables con dominio D. entonces la graficas de f es el conjunto de todos los puntos (x,y,z) en R3, tal que z=f(x,y)  y (x,y) esta en el dominio D

* la grafica de f(x,y) es una superficie en R3

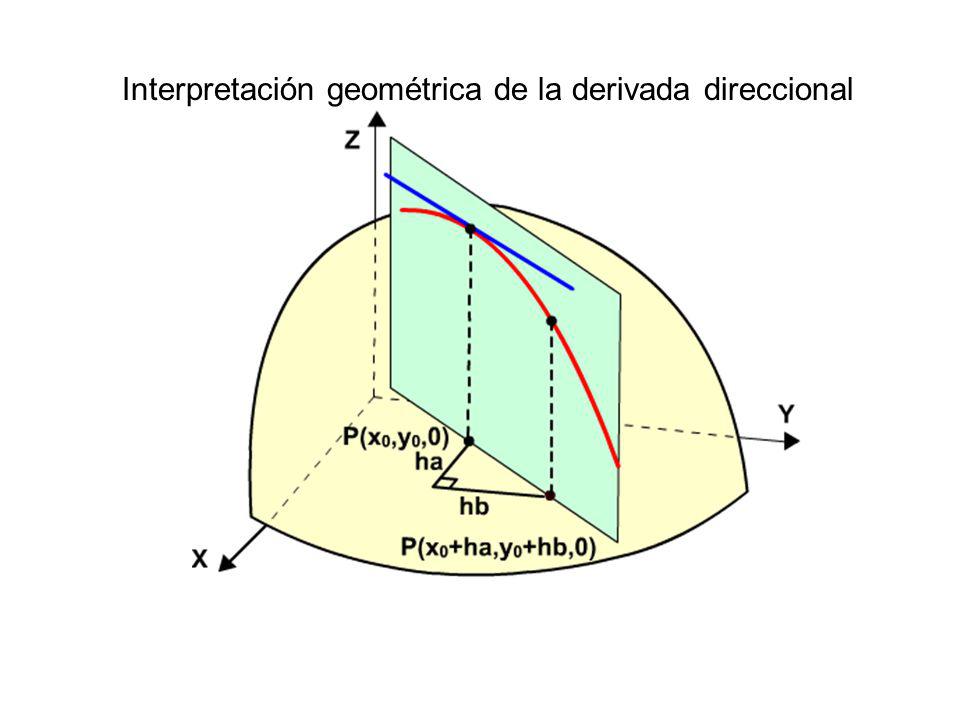
 DERIVADA DIRECCIONAL:
Como ya se estudio anteriormente el criterio de la derivada parcial, que era la razón de cambio de cada  cada, en este tema  se tomara en cuenta estas derivadas parciales, pero de todas las variables independiente y  del unitario de un vector que se dará como  dato en  futuros ejercicios.
Se une a cada derivada parcial en  un vector, dicho vector se lo  denomina gradiente.
Analiticamente la derivada direccional viene dada por :

http://slideplayer.es/slide/1629127/

NOTA 1: Se dice que si  la función tiene derivada en cada una de sus variables independientes entonces f  tiene una derivada direccional en la dirección de cualquier vector  unitario U.

1.1 .-VECTOR GRADIENTE: como ya se menciono antes el vector gradiente es  un vector que tiene la caracteristica de tener como  componentes las derivadas parciales de cada  uno de sus variables independientes, matematicamente el vector gradiente es :

Según la nota uno se puede deducir matemáticamente que la derivada direccional de una función con respecto a un vector unitario U  es el producto punto entre dicho vector unitario  y  el gradiente de la función.

NOTA 2:  En la teoría anterior se presento sustento matemático pero tan solo para dos variables, cabe mencionar que el teorema se cumple para n variables.

Formula de la derivada direccional para una función de tres variables.

NOTA 3: Se puede encontrar en futuros ejercicios postulados que pidan la direccion en la cual la funcion crece o decrece mas rápido, para ellos hay dos teoremas que dicen:

• El valor máximo de la derivada direccional  es el modulo del gradiente de la función, pero para que sea máximo el vector U debe tener la misma dirección que el gradiente. Caso contrario se dice que el valor sera mínimo.

2 .- VALORES MÁXIMOS  Y MÍNIMOS

http://geneura.ugr.es/~jmerelo/tutoriales/heuristics101/

Como en calculo de una variable se aprendió, se puede saber la forma de una función con sus derivadas, se aprendió a gráficar y para ello se necesitaba saber los puntos críticos de la función analizada (máximos  y mínimos) .

Ahora en calculo de varias variables este método de utilizar las derivadas no  cambia pero se deben tomar en cuenta mas factores que ayuden a la comprensión analítica de la función que se analizará.

Según la función que se este analizando, dicha función puede tener varios cambios de dirección en su forma, en cada cambio de dirección se generara un punto tope en el cual mencionado punto sera el mayor a todos los puntos que lo rodean a estos puntos se los denominan Maximon  o Minimos relativos.

Ahora en ejercicios futuros se pedirá el  Máximo o  Mínimo Absoluto  y este  no  es mas que el mayor de los Máximos  o  Mínimos relativos. 

MÁXIMOS Y MÍNIMOS RELATIVOS:

Máximo: Una función tiene un máximo relativo en el punto (a,b) si la funcion es menor o igual al valor de la función evaluada en el punto (a,b) 

Minimo: Una función tiene un mínimo relativo en el punto (a,b) si la función es mayor o igual al valor de la función evaluada en el punto (a,b)

2.1 .- PRUEBA DE LA PRIMERA DERIVADA

Utilizando derivadas se puede concluir que una función tiene un máximo  o mínimo relativo en (a,b)  suponiendo que sus derivadas de primer orden existen en ese punto, entonce:

2.2 .- PRUEBA DE LA SEGUNDA DERIVADA

Suponiendo que la segunda derivada parcial de cada variable existe y son continuas en un disco de centro  (a,b) ,la naturaleza del punto estacionario se puede determinar mediante el signo algebraico de la segunda derivada y del determinante de la matriz Hessiana.

Sea (a,b) un punto estacionario en el campo escalar f(x,y) con derivadas parciales segundas continuas en un entorno de (a,b) .

Sea D(a,b) la matriz Hessiana de f  en (a,b).

Entonces se tiene:

NOTA: 

• SI  D=0 entonces este análisis no será valido y  se recurrirá a otros métodos de análisis.
• Si D<0 comment-0--="" de="" dice="" entonces="" hay="" nbsp="" punto="" que="" se="" silla:="" un="">

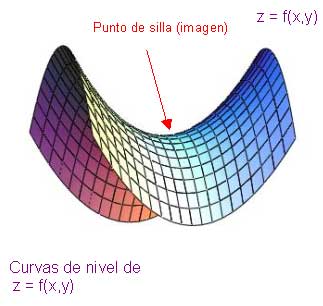
MÁXIMOS Y MÍNIMOS ABSOLUTOS:

Como se dijo  anteriormente el máximo o mínimo absoluto es el mayor de los máximos  y mínimos relativos, se calculan de la siguiente manera:

3 MULTIPLICADORES DE LAGRANGE

En los problemas de optimización, el método de los multiplicadores de Lagrange, llamados así en honor a Joseph Louis Lagrange, es un procedimiento para encontrar los máximos y mínimos de funciones de múltiples variables sujetas a restricciones. Este método reduce el problema restringido con n variables a uno sin restricciones de n + k variables, donde k es igual al número de restricciones, y cuyas ecuaciones pueden ser resueltas más fácilmente. Estas nuevas variables escalares desconocidas, una para cada restricción, son llamadas multiplicadores de Lagrange. El método dice que los puntos donde la función tiene un extremo condicionado con k restricciones, están entre los puntos estacionarios de una nueva función sin restricciones construida como una combinación lineal de la función y las funciones implicadas en las restricciones, cuyos coeficientes son los multiplicadores

Máximos  y mínimos condicionados:

SE llama un extremo condicionado de una función f(x,y) al máximo o mínimo de esta función alcanzado con la condición de que sus variables independientes enten relacionadas entre sí mediante la ecuación:

g(x,y)=o (Ecuación de enlace)

Para hallar los extremos condicionados se forma la llamada FUNCIÓN DE LAGRANGE.

Donde gama es una constante llamada MULTIPLICADOR DE LAGRANGE

Luego se determinan los Máximos relativos de la función de Lagrange.

Matematicamente se siguio probando el postulado y se llego a la conclución de que:

INTEGRALES MULTIPLES:

En calculo de una variable se aprendio que la integral de una función dentro de un intervalo (a,b) representa el area bajo la curva de dicha función.
Para dunciones de 2 variables la inegral representa el volumen bajo la superficie y sobre la region que se esta trabajando.

http://rodas.us.es/file/7cbe1663-15a4-35e1-308e-dafe50bbc603/2/tema7_ims_scorm.zip/page_06.htm

Tipos de regiones de integración



al momento de integrar se pueden presentar tres casos distintos

1. Regiones Rectangulares.
2. Regiones más generales.
3. Regiones generales. 

1. Regiones Rectangulares; 

En este tipo de regiones como  su nombre lo dice tienen la forma de un rectangulo, es decir tanto el eje x como  el eje y son constantes  y  los limites consecuentemente serán constantes.

Cabe recalcar que el orden en el que se desarrolle la integral no importa es decir, se puede comenzar con dx o con dy segun cual sea el camino más facil.

Regiones más generales.

En las regiones más generales se tienen dos partes, en un eje pasará lo anterior osea que sera una constante, mientras que en el otro será una funcion que no sera una recta.

Para resolver este tipo de regiones primero se desarrollara la de tipo variable y  luego la de tipo  constante, es decir los limites de la integral que esta más adentro seran funciones  y  los limites de la integral exterior seran constantes.

Cuando la función variable esta en función de x  y  la constante estará en el eje y:

Cuando la función variable esta en función de y  y  la constante estará en el eje x:

Regiones Generales:

En este caso la zona de trabajo ya  no  tendrá ninguna constante es decir en los dos ejes hay funciones variables .

El orden de resolución no importa ya que las dos son variables  y  el resultado seria el mismo.

El proceso de resolución  se realizara con  un cambio de variables y mediante la utilización del la matriz jacobiana.

DETERMINANTE JACOBIANA:

La determinante jacobiana se puede aplicar en funciones de cualquier número de variables independientes.

CAMBIOS DE VARIABLE:

Hay tres tipos de cambios de variable que son:

Coordenadas polares: Se las utiliza cuando  la región analizada es una circunferencia.

Coordenadas polares

Coordenadas Cilíndricas: Se las utiliza cuando la función analizada esta en el espacio y dos de sus variables están elevadas al cuadrado.

Coordenadas cilindricas

Coordenadas esféricas: Se la utiliza cuando la función esta en el espacio y las tres variables están elevadas al cuadrado.

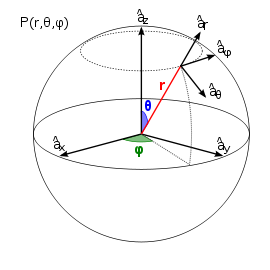Coordenadas esfericas

APLICACIONES DE LA INTEGRAL DOBLE: