Abril

Martes 19 de abril del 2016
clase # 1
* Indicaciones Generales
* Geometria analitica


clase # 2
                                VECTORIAL

generalmente la grafica de una funcion f(x,y)=0 representa una curva en el plano

*SISTEMA DE FUNCIONES IMPLICITAS
 F(x,y)=0
 G(x,y)=0
CADA UNA DE LAS FUNCIONES IMPLICITAS REPRESENTA UNA CURVA, POR TANTO LA SOLUCION DEL SISTEMA SERA UNO O MAS PUNTOS
 





 












 en R3 F(x,y,z)=0 funcion implicita de tres variables 
*caso especial 
F(x,y)=0, es una superficie en el espacio con generatriz paralela al eje Z 

 G(y,z)=0 superficie en R3 con generatriz paralela al eje X

H(x,z)=0
superficie en R3 con generatriz paralela al eje Y

SI F(x,y,z)=0
representa una superficie cuya generatri no es paralela a ningun eje coordenano
 *despejando
Z=f(x,y)     v        Z=f2(x,y)
y=g(x,z)     v        y=g2(x,z)
x=h(y,z)      v       x=h2(y,z)

geometricamente la solucion del sistema de funciones implicitas, representan curvas en R3

 LA RECTA 

ECUACIONES VECTORIALES DE LA RECTA (video)

clase # 3 

*ECUACIONES DE LOS PLANOS 

*EL PLANO EN EL ESPACIO 

ECUACION VECTORIAL DEL PLANO (video) 

*ECUACIONES IMCOMPLETAS DEL PLANO

Ec. del Plano con generatriz paralela al eje OZ

1) Si C=0 

    Ax + By + D = 0

    F(x,y) = 0

 

Ec. del Plano con generatriz paralela al eje OZ y que contiene al eje OZ

2) Si C=0 y D=0

    Ax + By = 0

   

Ec. del plano con generatriz paralela al los ejes OY y OZ

3) Si B=0 , C=0

    Ax + D = 0

  x=-D/A

  y= -D/B

  z=-D/C

 *ECUACION SEGMENTARIA DEL PLANO

 *ECUACION NORMAL DEL PLANO

NORMALIZACION DE LA ECUACION GENERAL DEL PLANO

Para normalizar la ecuación del plano se hace uso de un factor normalizante:

Que multiplicara a compenente de la ecuación, es decir:

El factor normalizante es:

                                                  
NOTA: El factor normalizante debe ser de signo contrario a D
DESVIACION DE UN PUNTO RESPECTO DE UN PLANO(δ)



δ es positiva cuando el punto M y el origen de coordenadas estan en lados opuestos al plano
δ es negativo cuando el punto M´ y el origen de coordenadas estan del mismo lado del plano

DISTACIA DE UN PUNTO AL PLANO

La distancia entre un punto y el plano debe representar su distancia perpendicular (figura).

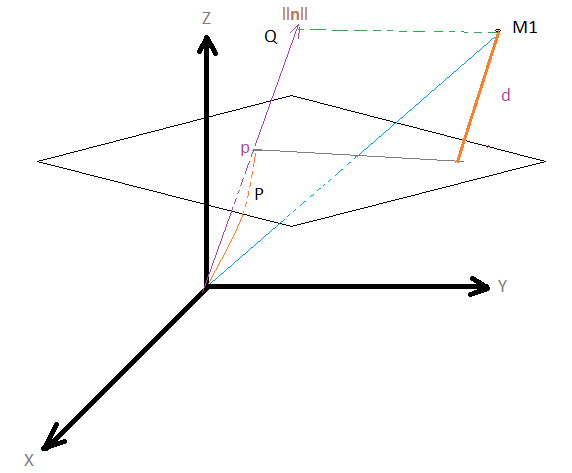Figura : Representación gráfica de la distancia entre un punto y el plano.
"Dicha distancia es perpendicular al plano".

La distancia viene determinada por:

PLANO DETERMINADO POR TRES PUNTOS

Para determinar la ecuación del plano se necesita o bien un punto y el vector normal o tres puntos (figura ), ya estudiado el primer caso ahora se determinara la ecuación por tres puntos:
Datos:

• P1(r1)
• P2(r2)
• P3(r3) 

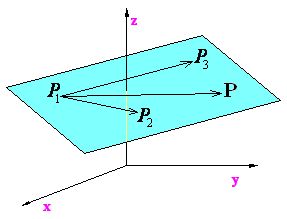Figura: Plano determinado por 3 puntos.

                                       
El plano viene determinado por la siguiente ecuación:

(r-r1).(r2-r1)x(r3-r1)=n

NOTA:
* si el produto mixto es igual al cero, entonces los 3 vectores involucrados SON COPLANARES.
*el producto mixto, geometricamente representa el volumen del paralelepipedo cuyas aristas son 3 vectores involucrados.


RECTA DETERMINADA POR DOS PLANOS

En un sistema de ecuaciónes de dos funciones se generaban curvas, pues bien en la intersección de dos planos se genera una recta (figura ), para representar de manera matemática a esta recta se tiene:
Datos:

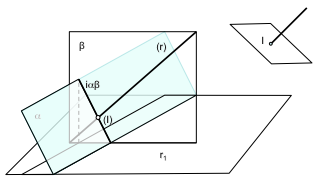Figura : Recta formada por dos planos.

                                         
Los vectores normales serán:

Haciendo un productos cruz entre estos dos vectores se obtiene un vector perpendicular a dichos vectores y este sera el vector director de la recta que se quiere calcular, obteniendo:

Luego se toma un punto de referencia con respecto a los planos esto se logra haciendo 0 a cualquiera de las variables en las dos ecuaciones, obteniendo un sistema de dos ecuaciones con dos incógnitas:

PARA X=0

Para determinar la ecuación de una recta se necesita el vector director y punto entonces las ecuaciones canónicas de la recta serán:

ECUACION DE HAZ DE PLANOS

Se denomina haz de planos a la intersección de infinitos planos que coinciden en una misma recta (figura ).

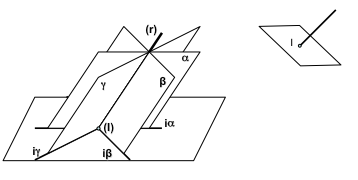Figura : Intersección de planos que coinciden en una misma recta.

Para determinar su ecuación tan solo se necesita las ecuaciones de dos planos.
Datos:

                                   


Multiplicando al plano 1 por alfa, al plano 2 por beta y sumando las dos ecuaciones se tiene:

Dividiendo toda la ecuación para alfa se obtiene:

Haciendo un cambio de variable y agrupando se llega a la ecuación requerida:

Ecuación del haz de planos.

El vector normal de esta haz de planos seria:

ECUACION VECTORIAL DE LA SUPERFICIE ESFERICA

superficie esferica

                                                      

  Superficies de segundo orden

Son todas aquellas que se representan por :

Se denominan también cuadráticas.

Escogiendo sistemas coordenados adecuados se puede simplificar su ecuación.

Para realizar su análisis y respectivamente su gráfica se realizan los siguientes pasos:

1. Intersección con los ejes coordenados.
2. Intersección con los planos coordenados.
3. Intersección con planos paralelos a los planos coordenados.
4. Trazado del bosquejo de la superficie de estudio.

Tipos de superficie.

a.- Elipsoide:

Ecuación:

representación tridimensional 

 Elipsoide.

b.- Hiperboloide de una hoja:

Ecuación

Representación tridimensional:

 

 

 

 

 

 

c.- Hiperboloide de dos hojas:

Ecuación:

Representación tridimensional:

 Hiperboloide de dos hojas.

d.-Paraboloide elíptico:

Ecuación:

Representación tridimensional:

Paraboloide eliptico

e.- Paraboloide hiperbólico:

Ecuación:

Representación tridimensional:

Paraboloide hiperbólico.

f.- Conos:

Ecuación:

Representación tridimensional

 conos.

g.- Cilindro:

Ecuación:

Representación Tridimensional:

 Cilindro.

NOTA: Las gráficas antes mostradas están en una posición, pero también pueden estar en dos posiciones mas dependiendo el signo de cada variable.